CHAPTER 12
Deviation from Size-Density
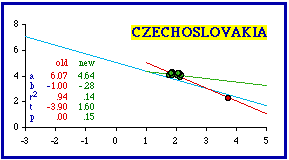
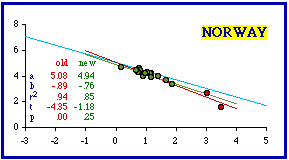
This table shows the nations from Table 5-2 which deviated from the world (and by now theoretical) slope of -2/3. We omitted the United Kingdom since it was the subject of studies reported in Chapter 7. As in Table 5-2, nations are ordered by their size-density slope, from the most positive (Italy) to the most negative (Sierra Leone).
Beginning with the most negative case first, it probably would have been wise originally to have ignored nations with so few divisions (here N = 4). It's hard to say what deviance (or conformity) means when so few units are involved. But since it was part of the set of nominally deviant nations, we analyzed it again anyway. Here is the Atlas entry[2] for Sierra Leone.
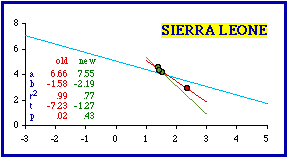
It is obvious that one district is different from the others. The "Western Area" is much smaller. It appears to be little more than a capital district (like Washington, D.C.), the location of the capital (Freetown, population 127,917). Its area of 327 square miles compares with, for example, such cities as Dallas, Indianapolis, Kansas City, New York, Phoenix or San Diego. It probably should have been excluded in the original study. One problem in the original study was the difficulty, in the early 1970s, of obtaining useful graphic output from computers. I had a program which would generate crude scatter diagrams on a printer, but the display was very limited (it wouldn't generate regression lines, for example). Had I generated scatter diagrams for each of the 98 nations studied, I might have discovered the problem with Sierra Leone (and a whole set of nations as we'll see below). Anyway, my interest back then was in the entire data set, not individual nations. The following figure shows the scatter diagram for Sierra Leone, together with the regression line (red) and the world regression line (light blue). Note that even though Sierra Leone "rejects" ß = -2/3, the dots fall close to the world line (This is reminiscent of some of the police car patrol districts in Chapter 7)
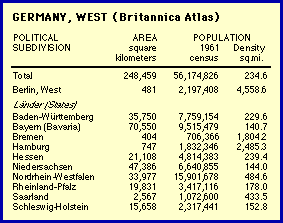
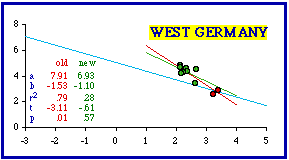
Clearly, as an outlier the Western Area (red dot) generates a very high coefficient of determination. Removal of this point makes the slope still more negative (green line, for the three remaining points, with very little variation in log d). So, in a way, the resulting set conforms even less to the hypothesized value of -2/3. Still, reduction of r-squared results in the probability value higher than the .05 rejection level. A similar problem occurred with the next most negative slope, West Germany. The Atlas entry[3] is shown in the accompanying table. In the original study I correctly excluded West Berlin, but I included two "States" which are really cities: Bremen and Hamburg. Cities are not products of territorial subdivision even if, like these or Washington, D.C., they might occasionally be given comparable legal status or simply comparable appearance in a data table. They should not be included in a test of a theory accounting for territorial subdivision.
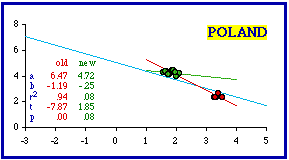
The scatter diagram for West Germany shows a similar pattern: As with Sierra Leone, removal of the outliers reduced the coefficient of determination and brought the probability well above the .05 level. In this case the new slope (green line) is actually closer to -2/3 after removal of the two city-states. I will not include further examples of Atlas entries since these two are sufficient to point out the problem of cities. The remaining "more negative" nations are presented with one scatter diagram only, showing the dropped cities as red dots Identification of all the cities dropped follows the graphs.
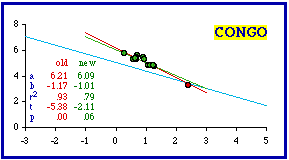
The cities ignored and the resulting probabilities are shown in the next table (the original probabilities have been computed exactly; the first table showed only critical values). In every case ignoring cities brought the data sets into conformity with ß = -2/3.
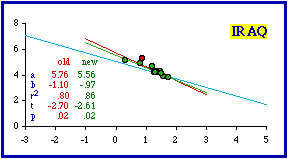
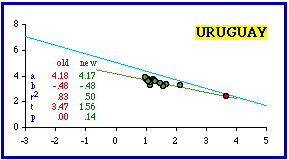
This technique did not work in the case of Iraq because Baghdad Uwa (Province) is not simply a city masquerading as a territorial division. Its 19,992 square kilometer area clearly makes it a territorial division. Its density of 74.6 is the highest in the nation, but the next lowest (Hillah, 55.2) is not that different. In any case, removal of the capital province doesn't bring Iraq into conformity (originally p = .01919; with removal p = .02406). Cities clearly should not be included in a test of a theory addressed to territorial divisions since the process through which they are created differs from that for territories. Cities grow outward from a point and need not be contiguous. This is usually not a problem when we are familiar with the data set being examined. We know, for example, that Washington, D.C., is not really a state, even when we find it included in a statistical table reporting state-level statistics. When you are unfamiliar with a country, however, it may be hard to tell which units are not territorial divisions. Often the only clue may be their extremely small size and usually very high density. This may seem to provide further support for the size-density law, but the problem is that statistical outliers like these tend to create very high correlation coefficients, and these tend toward rejection of the hypothesized -2/3 slope Nations Less Negative than -2/3 We continue with the nations less negative than theory would call for (more toward a slope of zero). Inclusion of cities as if they were territorial divisions can contribute to this condition, too. Montevideo was listed as one of Uruguay's departamentos even though it has an area of only 256 sq. mi. and a density of 4,582.5. It should have been excluded. When this city is dropped, the slope doesn't change, but the correlation coefficient does and Uruguay conforms.
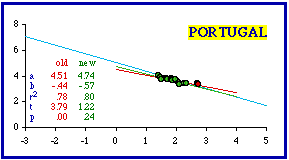
Portugal presents a different problem. Its most dense distrito is Porto (area = 2,282 sq. km.; density = 522.1). Its area (881 sq. mi.) is smaller than the smallest U.S. state (Rhode Island is 1,055 sq. mi.) but larger than a very large city (Los Angeles is 465.9 sq. mi.). It is listed as being only 38% urban. Clearly, Porto is a territorial division, not simply a city masquerading as one.
Furthermore, unlike Montevideo, Porto doesn't look like an outlier: it is in line with, and not too far removed from, the other distritos.. Removing it from the data set does improve things, from the theoretical point of view. The slope becomes more negative (from -0.44 to -0.47); the coefficient of determination doesn't change much (from 0.78 to 0.75); and the probability increases (from .00161 to .01105). Removing a second distrito (Lisbon) brings the entire data set into conformity with theory. Is this simply an exercise in curve-fitting? Clearly, we could go on removing non-fitting data-points until results meet theoretical expectation. But "cooking the data", if that is all we are doing, hardly constitutes a test of the theory. On the other hand, if the theory makes sense and already fits a wide body of data, it seems reasonable to see if removal of a few points can bring a deviant case into conformity. More importantly, if we can define some general patterns of deviation (erroneous inclusion of cities, most dense units, etc.), we may even be able to advance our understanding of the theory.
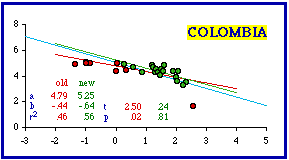
Eight units have been removed from the original Colombia data set. They differ from the remaining twenty-one departamentos. Three are listed as intendencías and five others are labeled comisarías. I don't know the significance of these classifications, but one unit (San Andrés y Porvidencia, area = 44 km.; density = 380.3) is extremely small and much denser than the departamentos. The other two intendencías and all the comisarías have extremely low densities (from 0.05 up to 2.2 per sq. km.; for comparison, Alaska's is about 1 per sq. km.; Australia and Nevada are about 10).
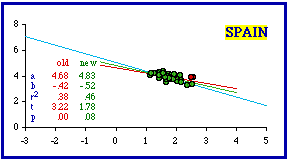
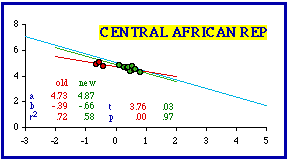
Exclusion of Spain's most dense provincía (Barcelona (372.2 per sq. km.) did not bring the set into conformity with theory (p = .01524). Removal of Barcelona and the penultimately dense Vizcaya (340.3) undoes the improvement (p = .00672). Simultaneous removal of Barcelona and Madrid (third most dense, 326.0) just passes the test for conformity with theory. The Central African Republic presented a new problem. Here the apparent outliers are low density prefectures. One listing is really a collection called "autonomous prefectures"; "it", if that is the word, is central among the three red dots. Removal of the three low density data-points produces the highest instance of conformity in the entire data set (b = -0.66; p = .97326).
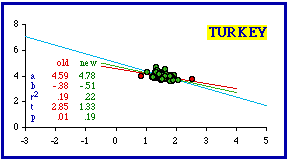
Theoretical conformity was achieved for sixty-five of Turkey's sixty- seven iller (provinces) by dropping cases from each extreme of density: the least dense (Hakkari, 7.1 per sq. km.) and the most dense (Istanbul, 329.5).
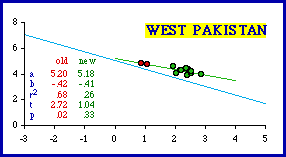
In the Atlas Pakistan is comprised of two provinces, West Pakistan (now simply Pakistan) and East Pakistan (now the separate nation of Bangladesh). The four divisions of East Pakistan conform to theoretical expectation, though with only four units and a low coefficient of determination, it may be important to say this more technically: East Pakistan "fails to reject" the hypothesis of a -2/3 slope. West Pakistan did not conform by the criterion employed here (b = -0.42; p = .02140). There were several outliers, however: the two mountainous units, Kalat and another, labeled "Quelta" in the table, "Quetta" on the map. Dropping these two didn't change the slope much but did reduce the coefficient of determination: r-squared went from .68 to .26. Whether this is "conformity" or simply "failure to reject" is debatable.
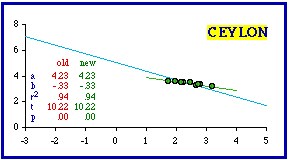
I could see no way of excluding units from Ceylon (now Sri Lanka) to achieve conformity with theoretical expectations. The slope is far from -2/3; the coefficient of determination is extremely high; there are no outliers responsible for either.
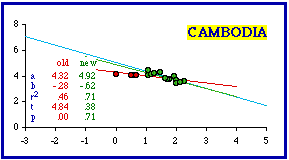
Removing the three least dense provinces from Cambodia produced conformity (b = -0.47; p = .11078). Taking out one more, which appears to be grouped with the others, resulted in much greater conformity for the remaining provinces even though the coefficient of determination increased as well (r-squared went from .58 to .71).
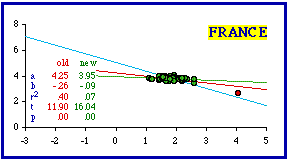
France proved intractable. There was only one obvious outlier département, Seine. It is small (480 sq. km.) and 100% urban (half its population is the city of Paris). Removing it leaves the remaining départements with a slope very near zero. Established in the Revolution, each "department was kept small enough so that its citizens could reach the Chef-lieu, or capital, in no more than a day's ride by horse-drawn vehicle".[4] Ironically, Napoleon later used these conveniently small divisions to maintain dictatorial control: the one- day travel rule applied to his soldiers as well as to the people.
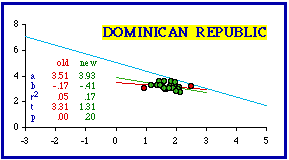
Importantly for the purpose of theory, if territorial divisions are created equal, in the territorial sense, there can be no size-density relation. If the dependent "variable" were indeed constant, there could of course be no relation between it and any independent variable. As was the case with Turkey, the Dominican Republic conformed to the theoretical expectation when both the least dense and most dense provincías were removed from the analysis. The least dense was Pedernales (9.8 per sq. km.); the most dense was Santo Domingo (358.4), separately listed in the table as the "National District", but not completely identified with the city (the district is only 79.4% urban).
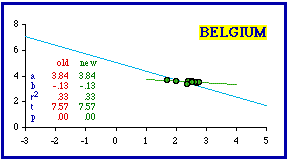
As is evident, there is nothing can be done to produce conformity in Belgium's nine provinces. You can remove the three least dense to obtain p = .04915, just below the criterion for conformity (b = -0.28; r- squared = .50). But that takes away a third of all the units, and does so for no reason other than to fit the curve (the reduced N makes the difference).
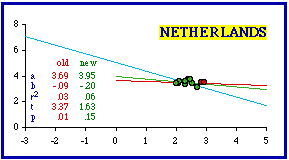
The Netherlands, like Belgium, consists of very few units to begin with. Dropping the two most dense provinces achieves theoretical conformity, but it does so with a significantly further reduced N and an extremely low coefficient of determination.
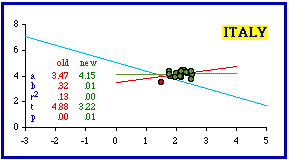
Italy appears to have only one outlier, the least dense of its regioni, Valle d'Aosta. Removing it, however, doesn't do much for us. The slope becomes virtually flat (b = 0.01). In spite of the fact that the coefficient of determination nearly disappears (r- squared = .00023), the theoretical expectation is rejected (p = .00538).
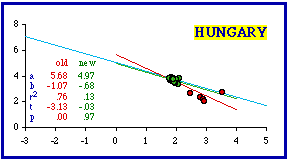
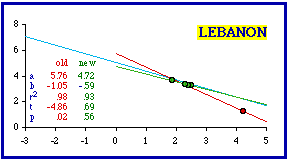
The results in this section are summarized in the following table. As in the preceding section, removal of very few units often results in theoretical conformity. Accounting for this will be the topic of the next chapter.
Appendix — Why the .05 Level? Since I raised some question (in the Appendix to the preceding chapter) to using the "p < .05" criterion, it is reasonable to ask why I use it here to decide about "conformity" to the hypothesis. I continue quoting the source from the previous Appendix. [5] The choice of a level of significance ... will usually be somewhat arbitrary since in most situations there is no precise limit to the probability of an error of the first kind that can be tolerated. It has become customary to choose ... one of a number of standard values such as .005, .01 or .05. There is some convenience in such standardization since it permits a reduction in certain tables needed for carrying out various tests. Otherwise there appears to be no particular reason for selecting these values....In this research I am not simply testing a null hypothesis. The size- density hypothesis is, first of all, not null: it asserts a definite, explicit, precise -2/3 relationship between variables. It emerged empirically, as the world regression line in the international study (Chapter 5), and is theoretically derivable (Chapters 8 and 10). It is supported with research involving other, cross-cultural territorial divisions (Chapter 6):
NOTES: [1] Douglas R. McMullin, "Urbanization and Territorial Subdivision: An Analysis of Nations which Deviate from the Size-Density Hypothesis", M.A. thesis, Department of Sociology, Western Washington University, 1981. The results are reported in G. Edward Stephan, Douglas R. McMullin and Karen Stephan, "Statistical and Historical Analyses of Nations which Deviate from the Size-Density Law", Demography, 19:567-76. 1982. [2] Britannica World Atlas. 255, London: Encyclopedia Britannica, Inc. 1967 [3] Britannica World Atlas. 223. [4] Charles Breunig, The Age of Revolution and Reaction,: 1789-1850, New York: Norton, 1970. [5] E. L. Lehmann, Testing Statistical Hypotheses, 61-2, New York: Wiley, 1959. |