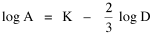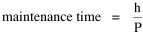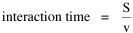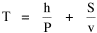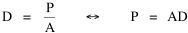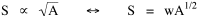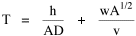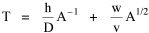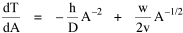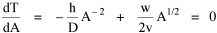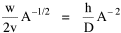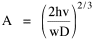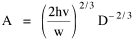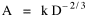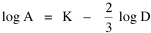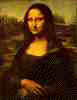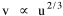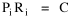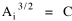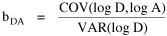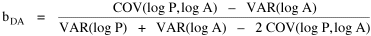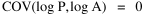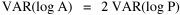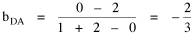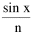|
CHAPTER 8
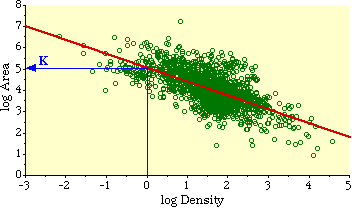
Size-Density from Time-MinimizationPhilosophy is written in this grand book — I mean the universe — which stands continually open to our gaze, but it cannot be understood unless one first learns to comprehend the language and interpret the characters in which it is written. It is written in the language of mathematics, and its characters are triangles, circles, and other geometrical figures, without which it is humanly impossible to understand a single word of it; without these, one is wandering about in a dark labyrinth.I had been fascinated by the -2/3 slope since 1971 when I first observed it, or one statistically indistinguishable from it, in the "world regression line" (Chapter 5).
The line is pictured in Fig 8-1. We may write its formula as
Between 1972 and 1975 a number of studies produced size-density slopes which did not depart significantly from this -2/3 value. Each time it happened I wondered Why? I tried to derive the slope theoretically (i.e., mathematically, from initial assumptions), but I failed each time until Spring term, 1975, when I was working with Jay Callen. Dimensional Analysis: Time Jay had been doing a lot of work with "central place theory", much of which involves explaining empirical regularities in terms of least distance models.[1] As it happened, I had been re-reading Zipf's principal work in which empirical regularities were derived in accordance with his principle of least effort.[2] At some point in all this I recalled a remark made by Professor Anderson, in a graduate school seminar in mathematical modeling, to the effect that well-developed theoretical fields tend to select fundamental dimensions and define other quantities in terms of these. The classical example of such "dimensional analysis" is Newtonian Physics. Length is clearly a dimension, in a real sense the most basic one we have. With length, plus a few other dimensions defined in terms of length (e.g., time and mass — the distance a marker moves on a proper scale), other quantities can be defined as in the following table, the last column of which contains only s, m & t — length, mass and time:
Among other advantages, such reduction of all variables to one (or a few) dimensions makes it possible to rigorously "balance equations" dimensionally — have the same units on both sides of the equation, or specify the units for embedded "constants." Different sciences use different fundamental dimensions, e.g., Chemistry - energy; Economics - money (but see the "Labor Theory of Value" below). I recall Professor Anderson suggesting at some point in our conversations that one day, perhaps, time might prove to be a fundamental dimension in Sociology. I began to think about least-time. Economics seems limited, as a general social science: what would its least-cost model mean in primitive societies which lack a money economy? In a similar vein, what could Geography's least-distance theories contribute to an understanding of future societies with "beam me up" technologies? I realize these are fictional, but our transportation systems make our ancestors view of distance hopelessly out of date also. Primtive societies where money is meaningless, future societies where distance is meaningless — how do you theorize about both using the same social science model? Zipf's least-effort notion was a conscious attempt to combine monetary and distance (and other) costs, but it smacked of mixing apples and oranges (dollars + miles + sweat?), and it lacked rigor: how, exactly, do you measure (quantify) "effort"?
The solution, it seems to me, is to translate these disparate variables
into the single dimension of Time. If I know the average velocity
of a given transportation technology, it is easy enough to translate
distance into time (distance is time, multiplied by veloctiy;
But thought's the slave of life, and life time's fool; Thought's the slave of life (all life), and life is time's fool — it could as easily have been written by Marx, or any biologist for that matter. I don't understand why Sociology (other than the classic intro text by the Lenskis) doesn't begin with Biology as Auguste Comte originally suggested. It would be a small step from there, in the study of human or non-human social systems, to see how relevant time really is as a fundamental dimension. Just for fun, Table 9-2 contains a very small sample of Shakespeare's many other references to time. I once shut down an online literature search engine by trying to get it to list all his references to "time"; next time I tried it "time" had been removed from searches, treated as too common along with words like "the" and "is"):
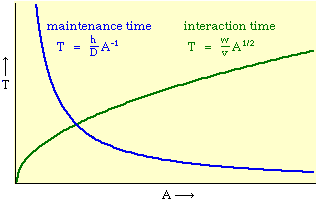
Time Minimization Theory Begin with this: Assume that social structures evolve in such a way as to minimize the time expended in their operation. Under this constraint, determine how large a county (or other territorial division) should be (in order to enforce law, maintain order, provide services, or whatever). One way of thinking about the value assumed by any variable is to assume it to be the result of contradictory forces: those tending to increase it, and those tending to decrease it. The larger a county is, other things equal, the more people there are to pay for its operations. On the other hand, the larger it is the harder it will be for distant citizens to reach, or be reached by, the county seat of government. Originally, the "maintenance" time of a county was donated by people who volunteered their time as its officials. With the growth of county government, however, the operations of a county are carried out by paid employees. The money required to pay them comes from taxes and other sources. Ultimately, however, we may imagine the money as the result of time expenditures by those making up the county (e.g., as taxed income, itself a product of time). Sharing the maintenance costs creates a centrifugal force, a tendency to increase the size the county, but as distance to the center increases the "interaction" time also increases, creating a centripetal force, a tendency to decrease county size. It seems reasonable to assume that actual county sizes represent a balance of these opposing tendencies, a minimizing of both "maintenance" and "interaction" times somehow taken together. We don't know what the maintenance time actually is, only that it represents some expenditure of hours, h. We also don't know how the burden is distributed among the citizens. We can refer to counties as being more or less costly in terms of average or per-capita time expenditures, where P is the population of the county. By a similar argument, ignoring the geographic distribution of the citizens within a county, we can specify an average interaction time where S is the average distance[4] to the county seat and v is the average velocity under existing transportation technology. The time expended in the operation of this social structure is the sum
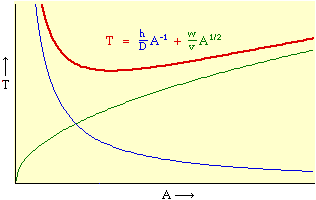
Now, how do we get from this expression to Eq. 1? We are trying to find an optimum value for A, the area served by the county, but A does not appear in Eq. 2, at least not directly. The definition of density is population divided by area The average distance to the county seat must be proportional to the square root of county area (by dimensional analysis a length in, e.g., miles must be proportional to the square root of an area in square miles), so with the constant of proportionality, w, we obtain the equation With these substitutions we can re-write Eq. 2 We can now write T as a function of A, treating D, h, w and v as (temporary) constants, These centrifugal and centripetal forces appear in Fig. 8-2, and Fig. 8- 3 indicates a minimum, least-time expenditure.
Taking the derivative[5] of T with respect to A gives us Setting the derivative equal to zero and solving for A produces We want to express Area as a function of Density, so we extract it from the right-hand term of Eq. 6 to obtain Reducing the constants to a single factor k The logarithmic transformation of Eq. 8, with K = log k, is Eq. 9 is identical to Eq. 1, the "world regression line" which we sought to derive theoretically. Thus, it follows directly from the assumption of Lack of Intentionality in Time Minimization
I want to emphasize something about
In contrast, I am explicitly not trying to specify rules to be
used by a rational decision maker. Nor am I in any way asserting that
people are inclined toward "rational" behavior. I am only trying to
account for the relationship described by
What I am putting forth here is pure theory, invention, fiction,
imagination. I am only trying to state the simplest assumption
which, if true, would account for the observed results. I
make no assertion of its truth (in fact, I don't think most people do
consciously minimize time, most of the time; they even "waste" it doing
things they "like" - see below). It is as if I had observed the relation
between temperature and pressure in a contained gas and began to speculate
about perfectly elastic tiny billiard balls whizzing around in perfectly
empty space, i.e., the kinetic theory of gases. In fact, the particles of
a gas tend to be not-perfectly-elastic, double-atom molecules, whizzing
around in not-perfectly-empty space. But it doesn't matter: the model is
good enough to make sense of the results (at the level of a simple gas
law). That is all I am doing with the assumption of
I belabor this point because I think Sociology tends to misunderstand the
nature of scientific theory. Whereas most scientific explanation accounts
for patterns in the recurrent behavior of very large numbers of events
(atoms, molecules, cells, organisms, species, planets, galaxies),
Sociology tends toward a highly
I illustrate this tendency in class lectures with reference to an exhibit
of 12th century Chinese scroll paintings I saw at the DeYoung Museum in
San Francisco when I was an undergraduate. The right-hand side of Fig 8-4
is a badly beat-up poster I still have from that exhibit. The two pictures
on the left are details from the
I was fascinated by this view of the place of humans in nature. Here are the sky, mountains, valleys, river gorges. There may be a forest or an orchard, a bridge. Often people are shown amidst the buildings or natural surroundings. Who are they? How are they grouped? The people in such a picture are subject to all sorts of laws: meteorological, biological, physical, nutritional, sociological. You don't have to enter their minds to account for their behavior any more than you have to enter the minds of molecules or monkeys to explain theirs. There is a structure in which these people, and thousands of others elsewhere and earlier, live out their lives. The other rooms in the museum at that time were populated with European works, mostly portraits, suggested here in Fig 8-5. Though some of them had great artistic merit, their view of human nature was very different from you get in Fig. 8-4 The entire emphasis here is on the individual and his or her mood or character or claim-to-fame. About the only hint you get that they even live in a world outside themselves might be in their title (the 15th Earl implies that there were 14 before him) or the placement of a pillar in the background (his pillar in his palace in his world).
There is a similar contrast in point-of-view in much literature. Moby Dick begins with the highly personal
Call me Ishmael. Some years ago—never mind how long precisely—having little or no money in my purse, and nothing particular to interest me on shore, I thought I would sail about a little and see the watery part of the world. and ends after much struggle with Now small fowls flew screaming over the yet yawning gulf; a sullen white surf beat against its steep sides; then all collapsed, and the great shroud of the sea rolled on as it rolled five thousand years ago.
Huckleberry
Finn, though less cosmic, moves similarly from the unique to the
recurrent. It begins with "You don't know about me...." and concludes:
"... Aunt Sally she's going to adopt me and civilize me, and I can't
stand it. I been there before."
I don't see how anyone could theorize about human behavior when
humans are viewed solely as willing, "motivated" individuals.
(Isn't "motivation" or "motive force" what got all the
pre-Galilean physicists back to Aristotle confused with regard to rest
versus motion?) Each individual is just that: a
genetically unique entity which, even if it were cloned a
thousand times, would still be unique in terms of subsequent
individual experience and personal "motivation". Predicting
behavior would be a matter of getting to know that individual
well enough to guess the next move correctly. The knowledge would
not generalize beyond that individual psyche. Your intense love
of football probably has little to say about mine for opera; your
need to golf has little to do with my need to solve puzzles. If
science is the study of recurrent events, then it has
nothing to say about individuals and their "likes" or "wills" or
"wants" or "motives". It should rather focus on the "common
denominator" which by assumption underlies all recurrent actions
and their patterns, something such as
A theory of human behavior which "makes sense" at an individual level
(rational choice or libidinal repression) ought to be suspect. Theories
should account for patterns which appear in macro-level data. A
theory like time-minimization should not be judged in terms of intuitive
"reality"; it need only account for the empirical finding better than
any competitor.
Publishing the Derivation
I submitted the derivation to the American Sociological
Review on April 8, 1975. The rejection arrived on June 9. One
reviewer had no opinion regarding publication, but did offer some hints
for tightening the presentation. The other wrote that
But theory is imaginary. When a theory is confirmed by direct
observation (e.g., cell theory through the microscope, the presence of
Neptune or Pluto with a telescope) it is no longer theory but fact. A
"truly operational model", as this reviewer seems to mean the words,
would be a description of an actual county. Is that even science? It
certainly isn't theory. The same reviewer didn't add to his credibility
when he pointed out that I hadn't "defined little d in the fraction
dT/dA" (the left side of Eq. 5 in the derivation above), and, even if I
had, it should be canceled from the fraction.[6]
After fruitless argument over these points with the ASR, I
submitted the paper to the American Journal of Sociology, January
16, 1976. It was rejected April 15. One referee described it as a
"useful fragment that ties together your previous work quite well" (you
could make the same remark about Newton's laws of motion). A second
found "work on area-density less than inspiring" (an interesting
criterion for judging scientific work). I asked for reconsideration and
received some discussion about the determinants of density (my
independent variable) and the statement
I mentioned the attention Durkheim had paid to precisely this topic (Chapter 4) and got nowhere, the final
rejection coming October 5, 1976.
I wrote back on January 10 commenting only that, for a purportedly
interdisciplinary scientific journal, I saw very little social science
in Science. On January 18 I received the reply
Nothing further by way explanation or commentary. I was ecstatic. It was
published the following April.[7] I have
received more, and more interesting, communication as a result of this
very brief publication in Science than I have from all my other
publications in Sociology journals combined. I have reproduced the article here, retaining as much of the original typography as possible (I couldn't create fully justified paragraphs however).
Earlier Derivations
Jay Callen has, over the years, brought to my attention three earlier
studies from other parts of the world which derive relations identical
or related to Eq. 1:
* In England, using a least-distance assumption, Palmer[8] derived
* Earlier, in Greece, also using a least-distance model (which he
equated with least-effort) Virirakis[9]
produced
* Earlier still, in Poland, Mycielski and Trzeciakowski,[10] in a derivation too long to be described
here, start from cost considerations and propose a method for locating
gasoline service stations efficiently (at least by their criteria). The
authors pass en route through two equations (on p. 68) compatible
with Eqs. 8 and 9.
Size-Density from Random Numbers
Consider the size-density regression coefficient, the covariance of
log D and log A, divided by the variance of log D:
NOTES:
[1] e.g., Ronald Abler, John S. Adams and Peter Gould,
Spatial Organization: The Geographer's View of the World,
Englewood Cliffs, NJ: Prentice-Hall, 1971.
[2] George K. Zipf, Human Behavior and the
Principle of Least Effort. Cambridge, MA: Addison-Wesley, 1949.
[3]
Henry IV, Part I, V, iv, 81-82. In all of Shakespeare's gloomy
references to time's ruination (see Table 8-2) he seems to exempt only
love:
[4] I follow the practice in physics of letting
S represent distance since d has special mathematical
significance and l ("ell" for "length") is easily confused with
the numeral representing unity.
[5]
Minimization: this will be in the methodological appendix.
[6] As any first-quarter calculus student knows dy/dx is just
a symbolic way of saying the derivative of y with respect to x. it could
have been written y' or f'(x) rather than dy/dx. In particular, "little d" is not
a factor which can be "canceled". By the logic of my reviewer, the letter H
should be written as 1, since it looks like eleven divided by eleven. After
mentioning this review in a presentation to an audience of scientists, one
suggested that I should ask the reviewer to evaluate
[7] G. Edward Stephan, "Territorial Division: the
Least-Time Constraint Behind the Formation of Subnational Boundaries",
Science, 196:523-4, April 27, 1977.
[8] D. S. Palmer, "The Placing of Service Points to
Minimize Travel", Operational Research Quarterly, 24:121-123,
1973.
[9] John Virirakis, "Minimum Effort as a Determinant
of the Area, Population, and Density of Residential Communities",
Ekistics, 27:362-371, 1969.
[10] Jerzy Mycielski and Witold Trzeciakowski,
"Optimization of the Size and Location of Service Stations", Journal
of Regional Science, 5:59-68, 1963.
[11] The algebraic details of this argument will be
presented more fully in Chapter 10
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||