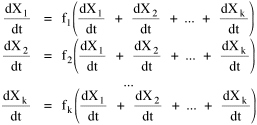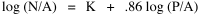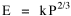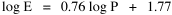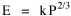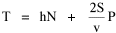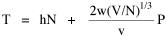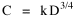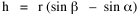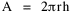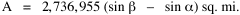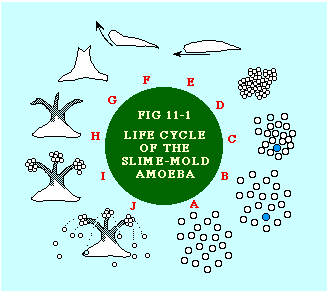
Interacting Populations in Biology

Human society can be regarded as an ecological system, or "ecosystem," something like a great pond, filled not with fish and frogs, plants and bacteria, but with workers and employers, gas stations and power companies, counties, states, and nations, churches and lodges, automobiles and refrigerators, wheat and steel and uranium, and all the innumerable "species" of social life, organizations, households, businesses and commodities of all kinds.... These populations of social species act and interact on each other in a great variety of ways. Some are mutually competitiveãthe more television sets, the fewer movie houses, both competing for "nutrition" in the form of the consumers' dollar. Some are mutually cooperative or complementary, like automobiles and gas stations. Some have parasitic relationships—the more cops, the fewer robbers, but the more robbers, the more cops!

Kenneth Boulding, Principles of Economic Policy, p.15

When I was still an undergraduate at San Francisco State I developed an interest in the structure of animal communities. Both Comte and Durkheim suggested that the study of such communities could be useful for the development of Sociology, and I took the suggestion seriously. After all, we and other social animals must share some organizing principles in common, whatever we believe may in addition distinguish us from them.

Back then I read Schaller's account^[1] of the mountain gorilla and Wheeler's much earlier one on ants^[2] and on social insects in general.^[3] I related Sociology's "human ecology", as developed by Park^[4], Quinn^[5] and Hawley^[6], to Allee's ^[7] animal ecology and Odum's ^[8] general ecology. Among other things, I noted in all this a simple pattern in human behavior which paralleled one observed in many animal groups, a simple pattern I have come to call the "law of equidistant spacing".

The bus I rode from San Francisco State to my apartment in Haight- Ashbury arrived empty at the pick-up point, having discharged all its outbound passengers at the Stonestown Shopping Center a block away. If I boarded while the bus was still nearly empty, I could rush to the back seat and, from there, observe new arrivals as they chose their seats. These people appeared to be exercising "free will" — they looked around before sitting down, sometimes uncertainly, sometimes walking past a seat then returning to it. Even so, I could predict the seat they would "choose" while they were still up front paying their fare, before they even looked into the seating area. People (or pairs of them) tend to select seats equally distant from others already occupied. My "equidistant" predictions were correct perhaps 85-90% of the time. You can test this law with a counter example — try sitting immediately next to someone you don't know on a nearly empty bus!

I still use my law of equidistant spacing, which you can observe in birds sitting along a roof or telephone wire or among amoebas grazing on a bacterial field (see below), in introductory courses to suggest that "free will" need not be incompatible with sociological laws. All that is needed is an absence of conscious interaction (in the bus case people who don't know each other) or the presence of very large numbers so that local thought/will, behavior and interactions have minimal effect on the aggregate pattern.

I supplement it with more immediate examples. When the sun comes out in Bellingham WA, students spread out on the lawn below my fifth floor office window like lizards sunning themselves on the rocks^[9]. Should several of them leave for class, I can predict where their successors will "choose" to lie by invoking my law of equidistant spacing. I have noticed that seating in restaurants can be problematic because of the same law: asking to share a table in the smoking section of the University coffeeshop, when there may be empty tables immediately nearby in the non-smoking section, constitutes a form of "invasion", making both the asker and the sitter uncomfortable.

In trying to find out how far down(?) the evolutionary ladder I could find social life, I came across Bonner's work^[10] on the "slime mold amoeba". I found these creatures fascinating, as do apparently many biologists: ^[11]

The remarkable life cycle of the slime mold Dictyostelium, the best-known member of the Acrasiales, is of general interest to biologists because it provides a model system of a developing multicellular organism that can be experimentally manipulated with relative ease. For sociobiologists it has the more special attraction of displaying perhaps the most advanced social behavior of single-celled organisms — the aggregation of the myxamebas that initiates the multicellular half of the life cycle.

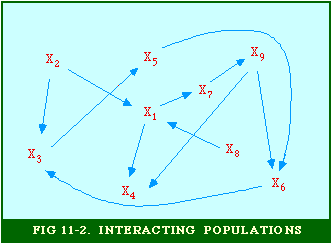
As single cells they behave like true amoebæ, grazing (equidistantly) on bacteria fields and dividing frequently (A). When food runs out for a given amoeba (say the blue spot in B), it becomes the focal point for mass migrations of others. The resulting cluster forms a sausage-like slug, as big as 2 millimeters in length (E). "It" behaves like a multicellular organism, with distinct head end, moving slowly toward heat and light.^[12] One or two weeks later "it" turns upright (F) forming a fruiting body, with some of the former amoebæ forming a base and stalk (H), others forming spore-bearing spheres (I) at the top. The spores subsequently spray outward (J), emerging later as single cells, and the cycle repeats.

In graduate school I tried to submit a 50-60 page paper on animal communities as part of the assignment for a seminar entitled "Social Structure and Process". It was rejected outright: the topic could be of no interest to sociologists. I nevertheless remained intrigued by what faculty referred to as sub-human social structures, particularly in seminars on the history of social thought. So much early social philosophy and 19th century sociological theory was taken up with the analogy between society and the organism, but I found it extremely useful to suggest a slightly different one, between society and an ecosystem. In another arena, teaching intro sociology courses, I enjoyed telling well-scrubbed fraternity and sorority types in my classes about the ecological system we carry around on and in our bodies.^[13]

I continued my interest in animal societies after arriving at Western, publishing two articles which suggested that the ecological system might serve as a paradigm for the quantitative analysis of human society.^[14] Central to each was the notion of a set of interacting populations, as illustrated with the nine species in Fig. 11-2. Here, species X₁ is dependent upon species X₇ which, in turn is dependent on species X₉, and so on. "Dependent on" usually means a predator-prey relation, but it could also refer to parasite- host, symbiotic or commensalistic relations.

This general interdependence can be described by the set of simultaneous equations, the ecosystem:

(1)

I don't mean to suggest that Sociology should attempt to find the exact form of such functions as Eqs. 1, or that it should only concern itself with the relation between human and non-human species. What I am suggesting is that we might benefit from thinking of society itself as a set of interacting populations. Consider a university as a small society: so many students producing so many student credit hours which generate so many faculty positions; so many dorm rooms, class rooms, recreation facilities, parking places, etc. It seems a useful way to think of "social structure".

Almost from the beginning of my interest in non-human social structure, the most influential work I came across was Wynne-Edwards' Animal Dispersion in Relation to Social Behavior.^[15] One of the primary thrusts of this work is to argue that much social behavior previously thought to be connected with mating (a Freudian influence?) was in fact connected with regulating demographic pressure on the food supply (a Marxian/Malthusian influence?).

Dawn-and-dusk bird song, for example, occurs even at times when mating is not taking place; its purpose, rather than broadcasting appeal to potential mates, appears rather to be to serve as a census of bird density, an indication to others whether to land or continue flying to other feeding sites. The hierarchy ("pecking order") has a similar demographic function: it identifies the surplus individuals who must leave should the food supply become too low to support the existing group. The "willing" exit of the surplus prevents a "war of each against all" which could wipe out the group. The traditionally claimed libidinal and power motives behind animal behavior prove far less important to group survival than does regulation of population-density vis-a-vis the food-density, says Wynne-Edwards. ^[16]

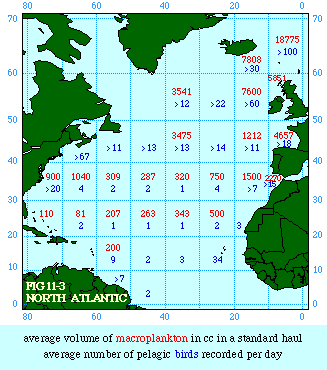
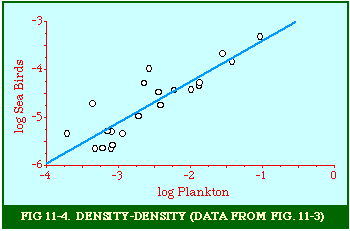
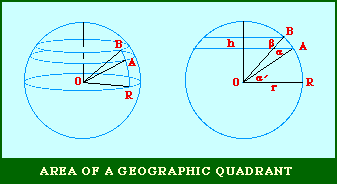
Fig. 11-3 is an adaptation of a map on the second page of Wynne-Edwards' book. It is based on Danish oceanographic expeditions made in search of the birthplace of freshwater eels, between 1913 and 1928. Standard hauls of macroplankton were taken all over the North Atlantic to be used as a broad index of the richness of surface waters, in terms of food for pelagic birds. The data are shown for 10deg. quadrants, upper figures showing the average volume of macroplankton in cc in a standard haul, and lower figures (bold face) the average number of birds recorded per day. He concludes:^[17]

In spite of the collective character of the data and the differences in season at which the different areas were sampled, the correlation that emerges between bird density and abundance of plankton is very strong: in numerical terms it can be expressed by a coefficient of +0.85. The probability that such a situation could have arisen by chance alone is negligible (P << 0.001).... The population-density in fact appears to be graded so that in every area it bears about the same constant average relation to the amount of plankton present.