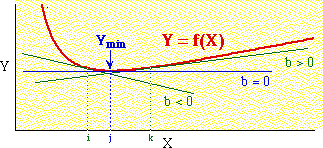
Differential Calculus. We have a curve describing the variable Y as some function of the variable X:

Various straight lines are drawn tangent to the curve Y = f(X). Only one of these can lie flat, i.e., have a slope of zero, the one shown here as b=0. Any line tangent to the left or right of that (X=i, X=k) will connect with higher values of Y. So at the value X=j, Y is at a minimum.

This is obvious from the graph. If we have the equation for Y we can also determine what the minimum is, provided there is one. For any curve described by the equation

where a is a constant and n is an exponent, the slope of a tangent line, called the "derivative", will be given by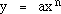

There are other rules (for logarithms and trigonometric functions, e.g.) presented in any elementary calculus text, but they need not concern us here.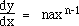

If the original equation contains several terms, differentiation is performed on each term separately:

Once we have the derivative we can set it equal to zero, then solve to identify the value of X which minimizes Y.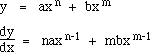

Technically, the derivative (slope of the tangent line) equal to zero applies when Y is at a minimum or a maximum (and also at what is called a point of inflection, not shown):

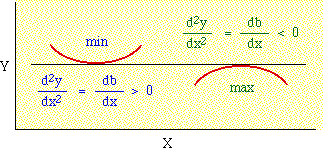
If the second derivative is positive (the change in slope is toward more positive values), then we have a minimum.